Wallpaper Groups
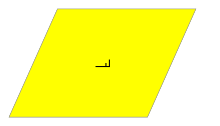
The group p1 contains only translations; there are no
rotations, reflections, or glide reflections.
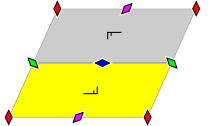
The group p2 contains four rotation centres of order two (180°), but no reflections or glide reflections.
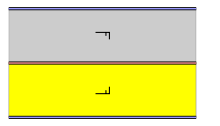
The group pm has no rotations. It has reflection axes, they are all parallel.
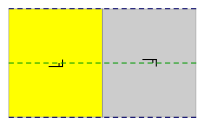
The group pg contains glide reflections only, and their axes are all parallel. There are no rotations or reflections.
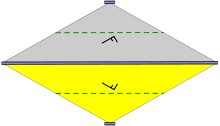
The group cm contains no rotations. It has reflection axes, all parallel. There is at least one glide reflection whose axis is not a reflection axis; it is halfway between two adjacent parallel reflection axes.
This group applies for symmetrically staggered rows (i.e. there is a shift per row of half the translation distance inside the rows) of identical objects, which have a symmetry axis perpendicular to the rows.
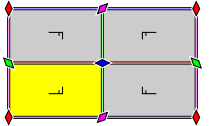
The group pmm has reflections in two perpendicular directions, and four rotation centres of order two (180°) located at the intersections of the reflection axes.
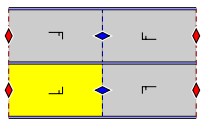
The group pmg has two rotation centres of order two (180°), and reflections in only one direction. It has glide reflections whose axes are perpendicular to the reflection axes. The centres of rotation all lie on glide reflection axes.
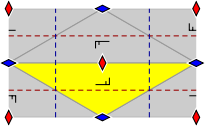
The group pgg contains two rotation centres of order two (180°), and glide reflections in two perpendicular directions. The centres of rotation are not located on the glide reflection axes. There are no reflections.
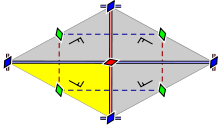
The group cmm has reflections in two perpendicular directions, and a rotation of order two (180°) whose centre is not on a reflection axis. It also has two rotations whose centres are on a reflection axis.
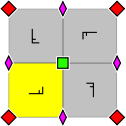
The group p4 has two rotation centres of order four (90°), and one rotation centre of order two (180°). It has no reflections or glide reflections.
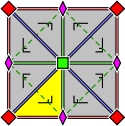
The group p4m has two rotation centres of order four (90°), and reflections in four distinct directions (horizontal, vertical, and diagonals). It has additional glide reflections whose axes are not reflection axes; rotations of order two (180°) are centred at the intersection of the glide reflection axes. All rotation centres lie on reflection axes.
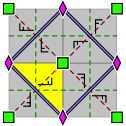
The group p4g has two centres of rotation of order four (90°), which are each other's mirror image, but it has reflections in only two directions, which are perpendicular. There are rotations of order two (180°) whose centres are located at the intersections of reflection axes. It has glide reflections axes parallel to the reflection axes, in between them, and also at an angle of 45° with these.
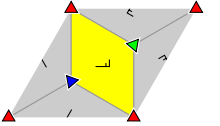
The group p3 has three different rotation centres of order three (120°), but no reflections or glide reflections.
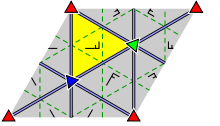
The group p3m1 has three different rotation centres of order three (120°). It has reflections in the three sides of an equilateral triangle. The centre of every rotation lies on a reflection axis. There are additional glide reflections in three distinct directions, whose axes are located halfway between adjacent parallel reflection axes.
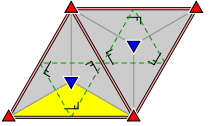
The group p31m has three different rotation centres of order three (120°), of which two are each other's mirror image. It has reflections in three distinct directions. It has at least one rotation whose centre does not lie on a reflection axis. There are additional glide reflections in three distinct directions, whose axes are located halfway between adjacent parallel reflection axes.
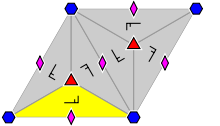
The group p6 has one rotation centre of order six, which only differ by a rotation of 60°; it has also two rotation centres of order three, which only differ by a rotation of 120° and three of order two (or, equivalently, 180°). It has no reflections or glide reflections.
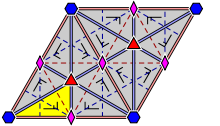
The group p6m has one rotation centre of order six (60°); it has also two rotation centres of order three, which only differ by a rotation of 60° (or, equivalently, 180°), and three of order two, which only differ by a rotation of 60°. It has also reflections in six distinct directions. There are additional glide reflections in six distinct directions, whose axes are located halfway between adjacent parallel reflection axes.